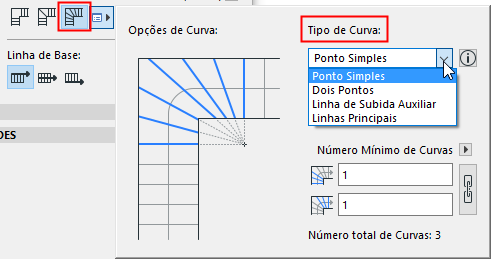
Tipos de Curva para Curvas com Passos Iguais

Passos Iguais significa que todos os passos na Escada são iguais, tanto nos degraus rectos como nos degraus em curva.

No painel Definições Escada - Geometria e Posicionamento:

Escolha um de quatro tipos de Curvas com Passos Iguais no pop-up: Ponto Simples, Dois Pontos, Linhas Principais e Linha de Subida Auxiliar.

Se aplicável, escolha Espelho ou Cobertor no Meio para o seu tipo de curva:

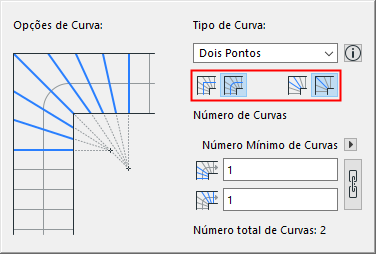
Curva com Passos Iguais: construída com Espelho ou Cobertor no Meio

À excepção do método Ponto Simples, todos os métodos têm duas versões dependendo se o centro da Curva é um Espelho ou um Cobertor.

Cada método é descrito em baixo:

Método de Ponto Simples

Método de Dois Pontos - Espelho no Meio

Método de Dois Pontos - Cobertor no Meio

Método de Linhas Principais - Espelho no Meio

Método de Linhas Principais - Cobertor no Meio

Método de Linha de Subida Auxiliar - Espelho no Meio

Método de Linha de Subida Auxiliar - Cobertor no Meio

Método de Ponto Simples

1.Passos iguais são medidos ao longo da linha de subida, a iniciar na base da escada. O passo mais próximo do ponto de viragem é considerado o Cobertor Central da Curva.

2.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

3.Linhas de Início e Fim são estendidas, o seu ponto de intersecção forma o ponto central da Curva.

4.Os pontos de passos iguais medidos ao longo da linha de subida são conectados ao ponto central, estas linhas forma os espelhos dos degraus em curva.

Método de Dois Pontos - Espelho no Meio

1.Centro da Curva é construído:

–Um Espelho único é construído do bissector da viragem.

2.Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar no ponto onde o bissector intersecta a linha de subida.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim são estendidas, os seus pontos de intersecção com o bissector formam os dois pontos centrais da Curva.

5.Os pontos de passos iguais medidos ao longo da linha de subida são conectados com o ponto central correspondente dos dois pontos centrais existentes. Estas linhas formam os espelhos dos degraus em curva.

Método de Dois Pontos - Cobertor no Meio

1.Centro da Curva é construído:

–Um Passo único é medido ao longo da linha de subida, em simetria com o bissector da viragem.

–O valor de Largura Mínima de Cobertor Afunilado é medido na aresta interior da viragem, em simetria com o bissector.

–Os pontos na aresta interior e os pontos na linha de subida definem o Cobertor Central.

2.Passos iguais são medidos ao longo da linha de subida, a iniciar no ponto onde as arestas do Cobertor Central intersectam a linha de subida.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim são estendidas. Arestas do Cobertor Central são também estendidas. Os pontos de intersecção destas linhas formam os dois pontos centrais da Curva.

5.Os pontos de passos iguais medidos ao longo da linha de subida são conectados com o ponto central correspondente dos dois pontos centrais existentes. Estas linhas formam os espelhos dos degraus em curva.

Método de Linhas Principais - Espelho no Meio

1.Centro da Curva é construído:

–Um Espelho único é construído do bissector da viragem.

–Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar no ponto onde o bissector intersecta a linha de subida.

–O valor de Largura Mínima de Cobertor Afunilado é medido na aresta interior da viragem, em ambas as direcções.

–Os pontos na aresta interior e os pontos na linha de subida definem os dois Cobertores Centrais.

2.Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar nos Cobertores Centrais.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim (as Linhas Principais) são estendidas. Arestas dos dois Cobertores Centrais são também estendidas.

5.Os pontos onde a Primeira Aresta de Cobertor Central e o Bissector intersectam a Linha de Início definem a distância X.

6.A distância X é media múltiplas vezes ao longo da Linha de Início. Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade inicial da curva.

7.Os pontos onde a Última Aresta de Cobertor Central e o Bissector intersectam a Linha de Fim definem a distância Y.

8.A distância Y é media múltiplas vezes ao longo da Linha de Fim. Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade final da curva.

Método de Linhas Principais - Cobertor no Meio

1.Centro da Curva é construído:

–Um Passo único é medido ao longo da linha de subida, em simetria com o bissector da viragem.

–O valor de Largura Mínima de Cobertor Afunilado é medido na aresta interior da viragem, em simetria com o bissector.

–Os pontos na aresta interior e os pontos na linha de subida definem o Cobertor Central.

2.Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar no Cobertor Central.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim (as Linhas Principais) são estendidas. Arestas do Cobertor Central são também estendidas.

5.Os pontos onde as Arestas do Cobertor Central intersectam a Linha de Início definem a distância X.

6.A distância X é media múltiplas vezes ao longo da Linha de Início. Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade inicial da curva.

7.Os pontos onde as Arestas do Cobertor Central intersectam a Linha de Fim definem a distância Y.

8.A distância Y é media múltiplas vezes ao longo da Linha de Fim. Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade final da curva.

Método de Linha de Subida Auxiliar - Espelho no Meio

1.Centro da Curva é construído:

–Um Espelho único é construído do bissector da viragem.

–Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar no ponto onde o bissector intersecta a linha de subida.

–A Linha de Subida Auxiliar é construída por afastamento da Linha de Subida para 200 mm da aresta interior.

–2/3 do Passo são medidos ao longo da Linha de Subida Auxiliar, em ambas as direcções.

–Os pontos na linha de subida e os pontos na Linha de Subida Auxiliar definem os dois Cobertores Centrais.

2.Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar nos Cobertores Centrais.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim (as Linhas Principais) são estendidas. Arestas dos dois Cobertores Centrais são também estendidas.

5.O comprimento do passo é medido múltiplas vezes ao longo da Linha de Início, a iniciar no ponto onde a Primeira Aresta do Cobertor Central intersecta a Linha de Início.

6.Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade inicial da curva.

7.O comprimento do passo é medido múltiplas vezes ao longo da Linha de Fim, a iniciar no ponto onde a Última Aresta do Cobertor Central intersecta a Linha de Fim.

8.Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade final da curva.

Método de Linha de Subida Auxiliar - Cobertor no Meio

1.Centro da Curva é construído:

–Um Passo único é medido ao longo da linha de subida, em simetria com o bissector da viragem.

–A Linha de Subida Auxiliar é construída por afastamento da Linha de Subida para 200 mm da aresta interior.

–1/2 do Passo é medido ao longo da Linha de Subida Auxiliar, em simetria com o bissector da viragem.

–Os pontos na linha de subida e os pontos na Linha de Subida Auxiliar definem o Cobertor Central.

2.Passos iguais são medidos ao longo da linha de subida, em ambas as direcções, a iniciar no Cobertor Central.

3.Linhas de Início e Fim da Curva – ou seja, o primeiro e o último passo recto – são construídas com base no parâmetro Número de Degraus em Curva.

4.Linhas de Início e Fim (as Linhas Principais) são estendidas. Arestas do Cobertor Central são também estendidas.

5.O comprimento do passo é medido múltiplas vezes ao longo da Linha de Início, a iniciar no ponto onde a Primeira Aresta do Cobertor Central intersecta a Linha de Início.

6.Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade inicial da curva.

7.O comprimento do passo é medido múltiplas vezes ao longo da Linha de Fim, a iniciar no ponto onde a Última Aresta do Cobertor Central intersecta a Linha de Fim.

8.Estes pontos são conectados aos respectivos pontos de passos iguais medidos ao longo da linha de subida. Estas linhas formam os espelhos da metade final da curva.

Segmentos de Curva

Em caso de um Segmento de Curva, o ponto central da parte da Curva da linha de subida é considerado o ponto inicial da Curva.

•Bissectores são construídos como a perpendicular à linha de subida através deste ponto.

•Passos Iguais são medidos a iniciar neste ponto.

•Larguras Mínimas de Cobertor Afunilado são medidas a iniciar na projecção deste ponto até à aresta interior.